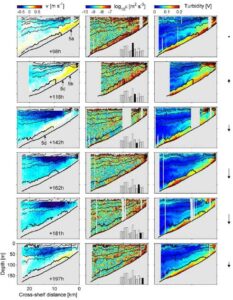
Successive transects of alongshore currents, turbulent dissipation rate and turbidity at 45N on the Oregon shelf.
A fundamental aspect of fluid mechanics is the no-flow boundary condition. A complicated transition from fluid in motion away from the boundary occurs across turbulent and viscous boundary layers. This forms an integral part of flows over continental shelves, where the additional contribution of the Coriolis force acts to induce an Ekman layer which moves fluid beneath a coastal current to the left in the northern hemisphere (and to the right in the southern hemisphere). Observations such as these provide a clear depiction of the cross-shelf motion of near-bottom fluid (outlined by the thick dark line in each panel). The progression (from top to bottom) shows onshore motion of near-bottom fluid halted and reversed as winds (arrow to R) decreased. Onshore motion resumed with increasing southward winds. This is an important component of coastal upwelling and is the mechanism by which offshore fluid laden with nutrients is brought onshore to be mixed upward into the euphotic zone to be utilized by phytoplankton.
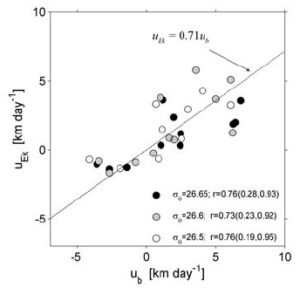
Scatter plot of cross-shore Ekman velocity (ordinate) computed from meaured bottom stress and a modified law-of-the-wall versus cross-shore velocity of BBL (abscissa) determined by tracking near-bottom fluid over successive transects.
Stratified bottom boundary layers require a modification to the law-of-the-wall typically used to describe the structure of velocity and turbulence within. This is because the stratification acts to attenuate the turbulence length scale which is allowed to increase without bound in neutrally-stratified boundary layers. Use of a modified law-of-the-wall permits a direct estimate of the Ekman transport in the bottom boundary layer which is in agreement with that determined by mapping the flow from successive transects (data points in the accompanying figure were derived from the figure above).
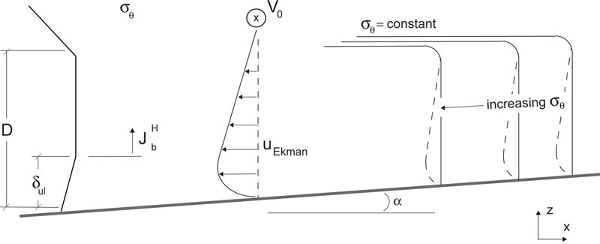
Structure of potential density and velocity above a bottom sloping upward to the east at a time when the current atop the Ekman layer flows northward and the density of the fluid in the bottom boundary layer decreases up the slope. Because the Ekman velocity profile has a near-bottom maximum, light fluid is drawn beneath dense fluid, initiating convection
Wind reversals during upwelling can lead to convectively-driven turbulence in coastal bottom boundary layers. We understand how this occurs at the sea surface when it is cooled (at night for example). What we have found is that the structure of the density (superadiabatic near-bottom layer) and the turbulence in convective bottom boundary layers is similar. An explanation of the motions leading to this is in the accompanying schematic.
Turbulence asymmetries in bottom boundary layer velocity pulses associated with onshore-propagating nonlinear internal waves., J. Phys. Oceanogr., 50(8), 2373-2391, doi: https://doi.org/10.1175/JPO-D-19-0178.1, 2020 (J. Becherer, J.N. Moum, J.A. Colosi, J.A. Lerczak and J.M. McSweeney).
Organization of stratification, turbulence and veering in bottom Ekman layers, J. Geophys. Res., 112, C05S90, doi:10.1029/2004JC002641, 2007 (A. Perlin, J. N. Moum, J.M. Klymak, M.D. Levine, T. Boyd and M. Kosro)
Irreversible vertical nitrate fluxes due to turbulent mixing in a coastal upwelling system, J. Geophys. Res., 110, C10S11, doi: https://doi.org/10.1029/2004JC002685, 2005 (B. Hales, J. Moum, P. Covert and A. Perlin).
Response of the bottom boundary layer over a sloping shelf to variations in alongshore wind, J. Geophys. Res., 110, C10S09, doi: https://doi.org/10.1029/2004JC002500,2005 (A. Perlin, J. N. Moum and J.M. Klymak).
A modified law-of-the-wall to describe velocity profiles in the bottom boundary layer, J. Geophys. Res., 110, C10S10, doi: https://doi.org/10.1029/2004JC002310, 2005 (A. Perlin, J.N. Moum, J.M. Klymak, M.D. Levine, T. Boyd and P.M. Kosro).
Convectively-driven mixing in the bottom boundary layer, J. Phys. Oceanogr., 34, 2189-2202, doi: https://doi.org/10.1175/1520-0485(2004)034%3C2189:CDMITB%3E2.0.CO;2, 2004 (J.N. Moum, A. Perlin, J.M. Klymak, M.D. Levine, T. Boyd and P.M. Kosro).
